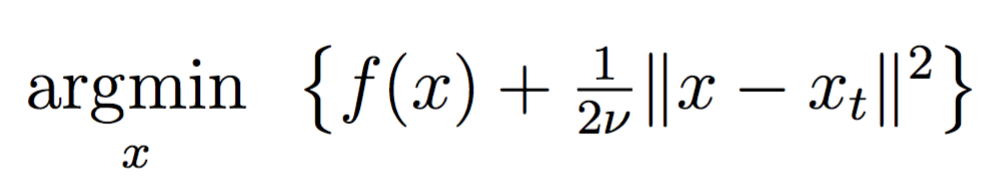Introduction

The proximal point method is a conceptually simple algorithm for minimizing a function \(f\) on \({\mathbb R}^d\). Given an iterate \(x_t\), the method defines \(x_{t+1}\) to be any minimizer of the proximal subproblem

for an appropriately chosen parameter \(\nu>0\). At first glance, each proximal subproblem seems no easier than minimizing \(f\) in the first place. On the contrary, the addition of the quadratic penalty term often regularizes the proximal subproblems and makes them well conditioned. Case in point, the subproblem may become convex despite \(f\) not being convex; and even if \(f\) were convex, the subproblem has a larger strong convexity parameter thereby facilitating faster numerical methods.

Despite the improved conditioning, each proximal subproblem still requires invoking an iterative solver. For this reason, the proximal point method has predominantly been thought of as a theoretical/conceptual algorithm, only guiding algorithm design and analysis rather than being implemented directly. One good example is the proximal bundle method (Lemarechal, Strodiot, and Bihain 1981), which approximates each proximal subproblem by a cutting plane model. In the past few years, this viewpoint has undergone a major revision. In a variety of circumstances, the proximal point method (or a close variant) with a judicious choice of the control parameter \(\nu>0\) and an appropriate iterative method for the subproblems can lead to practical and theoretically sound numerical methods. In this blog, I will briefly describe three recent examples of this trend:

• Episode 1: a subgradient method for weakly convex stochastic approximation problems (Davis and Grimmer 2017),

• Episode 2: the prox-linear algorithm for minimizing compositions of convex functions and smooth maps (Drusvyatskiy and Lewis 2016; Drusvyatskiy and Paquette 2016; Burke and Ferris 1995; Nesterov 2007; Lewis and Wright 2015; Cartis, Gould, and Toint 2011),

• Episode 3: Catalyst generic acceleration schema (Lin, Mairal, and Harchaoui 2015; 2017) for regularized Empirical Risk Minimization.

Each epsiode, discussing the examples above, is self-contained and can be read independently of the others. A version of this blog series will appear in SIAG/OPT Views and News 2018.

Notation

The following two constructions will play a basic role in the blog. For any closed function \(f\) on \({\mathbb R}^d\), the Moreau envelope and the proximal map are

respectively. In this notation, the proximal point method is simply the fixed-point recurrence on the proximal map:¹

Clearly, in order to have any hope of solving the proximal subproblems, one must ensure that they are convex. Consequently, the class of weakly convex functions forms the natural setting for the proximal point method.

A function \(f\) is called \(\rho\)-weakly convex if the assignment \(x\mapsto f(x)+\frac{\rho}{2}\|x\|^2\) is a convex function.

For example, a \(C^1\)-smooth function with \(\rho\)-Lipschitz gradient is \(\rho\)-weakly convex, while a \(C^2\)-smooth function \(f\) is \(\rho\)-weakly convex precisely when the minimal eigenvalue of its Hessian is uniformly bounded below by \(-\rho\). In essence, weak convexity precludes functions that have downward kinks. For instance, \(f(x):=-\|x\|\) is not weakly convex since no addition of a quadratic makes the resulting function convex.

Whenever \(f\) is \(\rho\)-weakly convex and the proximal parameter \(\nu\) satisfies \(\nu<\rho^{-1}\), each proximal subproblem is itself convex and therefore globally tractable. Moreover, in this setting, the Moreau envelope is \(C^1\)-smooth with the gradient

Rearranging the gradient formula yields the useful interpretation of the proximal point method as gradient descent on the Moreau envelope

In summary, the Moreau envelope \(f_{\nu}\) serves as a \(C^1\)-smooth approximation of \(f\) for all small \(\nu\). Moreover, the two conditions

and

are equivalent for the proximal point sequence \(\{x_t\}\). Hence, the step-size \(\|x_t-x_{t+1}\|\) of the proximal point method serves as a convenient termination criteria.

Examples of weakly convex functions

Weakly convex functions are widespread in applications and are typically easy to recognize. One common source of weakly convex functions is the composite problem class \(\mathcal{C}\):

where \(g\colon {\mathbb R}^d\to{\mathbb R}\cup\{+\infty\}\) is a closed convex function, \(h\colon{\mathbb R}^m\to{\mathbb R}\) is convex and \(L\)-Lipschitz, and \(c\colon{\mathbb R}^d\to{\mathbb R}^m\) is a \(C^1\)-smooth map with \(\beta\)-Lipschitz gradient. An easy argument shows that \(F\) is \(L\beta\)-weakly convex. This is a worst case estimate. In concrete circumstances, the composite function \(F\) may have a much more favorable weak convexity constant (e.g., phase retrieval (Duchi and Ruan 2017a, Section 3.2)).

1. (Additive composite) The most prevalent example is additive composite minimization. In this case, the map \(c\) maps to the real line and \(h\) is the identity function:

   \[\label{eqn:add_comp} \min_{x}~ c(x)+g(x).\]

   Such problems appear often in statistical learning and imaging. A variety of specialized algorithms are available; see for example Beck and Teboulle (2012) or Nesterov (2013).

2. (Nonlinear least squares)

   The composite problem class also captures nonlinear least squares problems with bound constraints:

   \[\begin{aligned} \min_x~ \|c(x)\|_2\quad \textrm{subject to}\quad l_i\leq x_i\leq u_i ~\forall i. \end{aligned}\]

   Such problems pervade engineering and scientific applications.

3. (Exact penalty formulations) Consider a nonlinear optimization problem:

   \[\begin{aligned} \min_x~ \{f(x): G(x)\in \mathcal{K}\}, \end{aligned}\]

   where \(f\) and \(G\) are smooth maps and \(\mathcal{K}\) is a closed convex cone. An accompanying penalty formulation – ubiquitous in nonlinear optimization – takes the form

   \[\min_x~ f(x)+\lambda \cdot {\rm dist}_{\mathcal{K}}(G(x)),\]

   where \({\rm dist}_{\mathcal{K}}(\cdot)\) is the distance to \(\mathcal{K}\) in some norm. Historically, exact penalty formulations served as the early motivation for the composite class \(\mathcal{C}\).

4. (Robust phase retrieval) Phase retrieval is a common computational problem, with applications in diverse areas, such as imaging, X-ray crystallography, and speech processing. For simplicity, I will focus on the version of the problem over the reals. The (real) phase retrieval problem seeks to determine a point \(x\) satisfying the magnitude conditions,

   \[|\langle a_i,x\rangle|\approx b_i\quad \textrm{for }i=1,\ldots,m,\]

   where \(a_i\in {\mathbb R}^d\) and \(b_i\in{\mathbb R}\) are given. Whenever there are gross outliers in the measurements \(b_i\), the following robust formulation of the problem is appealing (Eldar and Mendelson 2014; Duchi and Ruan 2017a; Davis, Drusvyatskiy, and Paquette 2017):

   \[\min_x ~\tfrac{1}{m}\sum_{i=1}^m |\langle a_i,x\rangle^2-b_i^2|.\]

   Clearly, this is an instance of the composite class \(\mathcal{C}\). For some recent perspectives on phase retrieval, see the survey (Luke 2017). There are numerous recent nonconvex approaches to phase retrieval, which rely on alternate problem formulations; e.g., (Candès, Li, and Soltanolkotabi 2015; Chen and Candès 2017; Sun, Qu, and Wright 2017).

5. (Robust PCA) In robust principal component analysis, one seeks to identify sparse corruptions of a low-rank matrix (Candès et al. 2011; Chandrasekaran et al. 2011). One typical example is image deconvolution, where the low-rank structure models the background of an image while the sparse corruption models the foreground. Formally, given a \(m\times n\) matrix \(M\), the goal is to find a decomposition \(M=L+S\), where \(L\) is low-rank and \(S\) is sparse. A common formulation of the problem reads:

   \[\min_{U\in {\mathbb R}^{m\times r},V\in {\mathbb R}^{n\times r}}~ \|UV^T-M\|_1,\]

   where \(r\) is the target rank.

6. (Censored \(\mathbb{Z}_2\) synchronization) A synchronization problem over a graph is to estimate group elements \(g_1,\ldots, g_n\) from pairwise products \(g_ig_j^{-1}\) over a set of edges \(ij\in E\). For a list of application of such problem see (Bandeira, Boumal, and Voroninski 2016; Singer 2011; Abbe et al. 2014), and references therein. A simple instance is \(\mathbb{Z}_2\) synchronization, corresponding to the group on two elements \(\{-1,+1\}\). The popular problem of detecting communities in a network, within the Binary Stochastic Block Model (SBM), can be modeled using \(\mathbb{Z}_2\) synchronization.

   Formally, given a partially observed matrix \(M\), the goal is to recover a vector \(\theta\in \{\pm 1\}^d\), satisfying \(M_{ij}\approx \theta_i \theta_j\) for all \(ij\in E\). When the entries of \(M\) are corrupted by adversarial sign flips, one can postulate the following formulation

   \[\min_{\theta\in {\mathbb R}^{d}}~ \|P_{E}(\theta\theta^T-M)\|_1,\]

   where the operator \(P_E\) records the entries indexed by the edge set \(E\). Clearly, this is again an instance of the composite problem class \(\mathcal{C}\).

References

Abbe, E., A.S. Bandeira, A. Bracher, and A. Singer. 2014. “Decoding Binary Node Labels from Censored Edge Measurements: Phase Transition and Efficient Recovery.” IEEE Trans. Network Sci. Eng. 1 (1):10–22. https://doi.org/10.1109/TNSE.2014.2368716.

Agarwal, A., and L. Bottou. 2015. “A Lower Bound for the Optimization of Finite Sums.” In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6-11 July 2015, 78–86. http://leon.bottou.org/papers/agarwal-bottou-2015.

Allen-Zhu, Z. 2016. “Katyusha: The First Direct Acceleration of Stochastic Gradient Methods.” Preprint arXiv:1603.05953 (Version 5).

Arjevani, Y. 2017. “Limitations on Variance-Reduction and Acceleration Schemes for Finite Sums Optimization.” In Advances in Neural Information Processing Systems 30, edited by I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, 3543–52. Curran Associates, Inc. http://papers.nips.cc/paper/6945-limitations-on-variance-reduction-and-acceleration-schemes-for-finite-sums-optimization.pdf.

Bandeira, A.S., N. Boumal, and V. Voroninski. 2016. “On the Low-Rank Approach for Semidefinite Programs Arising in Synchronization and Community Detection.” In Proceedings of the 29th Conference on Learning Theory, COLT 2016, New York, Usa, June 23-26, 2016, 361–82. http://jmlr.org/proceedings/papers/v49/bandeira16.html.

Bartlett, P.L., M.I. Jordan, and J.D. McAuliffe. 2006. “Convexity, Classification, and Risk Bounds.” J. Amer. Statist. Assoc. 101 (473):138–56. https://doi-org.offcampus.lib.washington.edu/10.1198/016214505000000907.

Beck, A., and M. Teboulle. 2012. “Smoothing and First Order Methods: A Unified Framework.” SIAM J. Optim. 22 (2):557–80. https://doi.org/10.1137/100818327.

Bottou, L., and O. Bousquet. 2008. “The Tradeoffs of Large Scale Learning.” In Advances in Neural Information Processing Systems, 161–68. http://leon.bottou.org/publications/pdf/nips-2007.pdf.

Burke, J.V., and M.C. Ferris. 1995. “A Gauss-Newton Method for Convex Composite Optimization.” Math. Programming 71 (2, Ser. A):179–94. https://doi.org/10.1007/BF01585997.

Candès, E.J., X. Li, Y. Ma, and J. Wright. 2011. “Robust Principal Component Analysis?” J. ACM 58 (3):Art. 11, 37. https://doi.org/10.1145/1970392.1970395.

Candès, E.J., X. Li, and M. Soltanolkotabi. 2015. “Phase Retrieval via Wirtinger Flow: Theory and Algorithms.” IEEE Trans. Inform. Theory 61 (4):1985–2007. https://doi.org/10.1109/TIT.2015.2399924.

Carmon, Y., J.C. Duchi, O. Hinder, and A. Sidford. 2017a. “‘Convex Until Proven Guilty’: Dimension-Free Acceleration of Gradient Descent on Non-Convex Functions.” In Proceedings of the 34th International Conference on Machine Learning, 70:654–63.

Y. Carmon, J.C. Duchi, O. Hinder, and A. Sidford. Lower bounds for finding stationary points I. Preprint arXiv:1710.11606.

Cartis, C., N.I.M. Gould, and P.L. Toint. 2011. “On the Evaluation Complexity of Composite Function Minimization with Applications to Nonconvex Nonlinear Programming.” SIAM J. Optim. 21 (4):1721–39. https://doi.org/10.1137/11082381X.

Chambolle, A., and T. Pock. 2011. “A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging.” J. Math. Imaging Vision 40 (1):120–45. https://doi.org/10.1007/s10851-010-0251-1.

Chandrasekaran, V., S. Sanghavi, P. A. Parrilo, and A.S. Willsky. 2011. “Rank-Sparsity Incoherence for Matrix Decomposition.” SIAM J. Optim. 21 (2):572–96. https://doi.org/10.1137/090761793.

Chen, Y., and E.J. Candès. 2017. “Solving Random Quadratic Systems of Equations Is Nearly as Easy as Solving Linear Systems.” Comm. Pure Appl. Math. 70 (5):822–83. https://doi-org.offcampus.lib.washington.edu/10.1002/cpa.21638.

Davis, D. 2016. “SMART: The Stochastic Monotone Aggregated Root-Finding Algorithm.” Preprint arXiv:1601.00698.

Davis, D., D. Drusvyatskiy, and C. Paquette. 2017. “The Nonsmooth Landscape of Phase Retrieval.” Preprint arXiv:1711.03247.

Davis, D., and B. Grimmer. 2017. “Proximally Guided Stochastic Sbgradient Method for Nonsmooth, Nonconvex Problems.” Preprint, arXiv:1707.03505.

Defazio, A. 2016. “A Simple Practical Accelerated Method for Finite Sums.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 676–84. Curran Associates, Inc. http://papers.nips.cc/paper/6154-a-simple-practical-accelerated-method-for-finite-sums.pdf.

Defazio, A., F. Bach, and S. Lacoste-Julien. 2014. “SAGA: A Fast Incremental Gradient Method with Support for Non-Strongly Convex Composite Objectives.” In Advances in Neural Information Processing Systems 27, edited by Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger, 1646–54. Curran Associates, Inc.

Defazio, A., J. Domke, and T.S. Caetano. 2014. “Finito: A Faster, Permutable Incremental Gradient Method for Big Data Problems.” In ICML, 1125–33.

Drusvyatskiy, D., and A.S. Lewis. 2013. “Tilt Stability, Uniform Quadratic Growth, and Strong Metric Regularity of the Subdifferential.” SIAM J. Optim. 23 (1):256–67. https://doi.org/10.1137/120876551.

D. Drusvyatskiy and A.S. Lewis. 2016. “Error Bounds, Quadratic Growth, and Linear Convergence of Proximal Methods.” To Appear in Math. Oper. Res., arXiv:1602.06661.

Drusvyatskiy, D., B.S. Mordukhovich, and T.T.A. Nghia. 2014. “Second-Order Growth, Tilt-Stability, and Metric Regularity of the Subdifferential.” J. Convex Anal. 21 (4):1165–92.

Drusvyatskiy, D., and C. Paquette. 2016. “Efficiency of Minimizing Compositions of Convex Functions and Smooth Maps.” Preprint, arXiv:1605.00125.

Duchi, J.C., and F. Ruan. 2017a. “Solving (Most) of a Set of Quadratic Equalities: Composite Optimization for Robust Phase Retrieval.” Preprint arXiv:1705.02356.

J.C. Duchi and F. Ruan. 2017b. “Stochastic Methods for Composite Optimization Problems.” Preprint arXiv:1703.08570.

Eldar, Y.C., and S. Mendelson. 2014. “Phase Retrieval: Stability and Recovery Guarantees.” Appl. Comput. Harmon. Anal. 36 (3):473–94. https://doi.org/10.1016/j.acha.2013.08.003.

Frostig, R., R. Ge, S.M. Kakade, and A. Sidford. 2015. “Un-Regularizing: Approximate Proximal Point and Faster Stochastic Algorithms for Empirical Risk Minimization.” In Proceedings of the 32nd International Conference on Machine Learning (ICML).

Ghadimi, S., and G. Lan. 2013. “Stochastic First- and Zeroth-Order Methods for Nonconvex Stochastic Programming.” SIAM J. Optim. 23 (4):2341–68. https://doi.org/10.1137/120880811.

Güler, O. 1992. “New Proximal Point Algorithms for Convex Minimization.” SIAM J. Optim. 2 (4):649–64. https://doi-org.offcampus.lib.washington.edu/10.1137/0802032.

Hazan, E., and S. Kale. 2011. “Beyond the Regret Minimization Barrier: An Optimal Algorithm for Stochastic Strongly-Convex Optimization.” In Proceedings of the 24th Annual Conference on Learning Theory, edited by Sham M. Kakade and Ulrike von Luxburg, 19:421–36. Proceedings of Machine Learning Research. Budapest, Hungary: PMLR.

Johnson, R., and T. Zhang. 2013. “Accelerating Stochastic Gradient Descent Using Predictive Variance Reduction.” In Proceedings of the 26th International Conference on Neural Information Processing Systems, 315–23. NIPS’13. USA: Curran Associates Inc. http://dl.acm.org/citation.cfm?id=2999611.2999647.

Juditsky, A., and Y. Nesterov. 2014. “Deterministic and Stochastic Primal-Dual Subgradient Algorithms for Uniformly Convex Minimization.” Stoch. Syst. 4 (1):44–80. https://doi-org.offcampus.lib.washington.edu/10.1214/10-SSY010.

Lacoste-Julien, S., M. Schmidt, and F. Bach. 2012. “A Simpler Approach to Obtaining an \({O}(1/t)\) Convergence Rate for the Projected Stochastic Subgradient Method.” Arxiv arXiv:1212.2002.

Lan, G. 2015. “An Optimal Randomized Incremental Gradient Method.” arXiv:1507.02000.

Lemarechal, C., J.-J. Strodiot, and A. Bihain. 1981. “On a Bundle Algorithm for Nonsmooth Optimization.” In Nonlinear Programming, 4 (Madison, Wis., 1980), 245–82. Academic Press, New York-London.

Lewis, A.S., and S.J. Wright. 2015. “A Proximal Method for Composite Minimization.” Math. Program. Springer Berlin Heidelberg, 1–46. https://doi.org/10.1007/s10107-015-0943-9.

Lin, H., J. Mairal, and Z. Harchaoui. 2015. “A Universal Catalyst for First-Order Optimization.” In Advances in Neural Information Processing Systems, 3366–74.

Lin, H., J. Mairal, and Z. Harchaoui. “Catalyst Acceleration for First-order Convex Optimization: from Theory to Practice.” arXiv preprint arXiv:1712.05654 (2017).

Luke, R. 2017. “Phase Retrieval, What’s New?” SIAG/OPT Views and News 25 (1).

Mairal, J. 2015. “Incremental Majorization-Minimization Optimization with Application to Large-Scale Machine Learning.” SIAM Journal on Optimization 25 (2):829–55.

Nemirovski, A. 2004. “Prox-Method with Rate of Convergence \(O(1/t)\) for Variational Inequalities with Lipschitz Continuous Monotone Operators and Smooth Convex-Concave Saddle Point Problems.” SIAM J. Optim. 15 (1):229–51. https://doi.org/10.1137/S1052623403425629.

Nemirovski, A., A. Juditsky, G. Lan, and A. Shapiro. 2008. “Robust Stochastic Approximation Approach to Stochastic Programming.” SIAM J. Optim. 19 (4):1574–1609. https://doi-org.offcampus.lib.washington.edu/10.1137/070704277.

Nemirovsky, A.S., and D.B. Yudin. 1983. Problem Complexity and Method Efficiency in Optimization. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York.

Nesterov, Y., and A. Nemirovskii. 1994. Interior-Point Polynomial Algorithms in Convex Programming. Vol. 13. SIAM Studies in Applied Mathematics. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611970791.

Nesterov, Yu. 1983. “A Method for Solving the Convex Programming Problem with Convergence Rate \(O(1/k^{2})\).” Dokl. Akad. Nauk SSSR 269 (3):543–47.

Nesterov, Yu. 2005. “Smooth Minimization of Non-Smooth Functions.” Math. Program. 103 (1, Ser. A):127–52. https://doi.org/10.1007/s10107-004-0552-5.

Nesterov, Yu. 2007. “Modified Gauss-Newton Scheme with Worst Case Guarantees for Global Performance.” Optim. Methods Softw. 22 (3):469–83. https://doi.org/10.1080/08927020600643812.

Nesterov, Yu. 2013. “Gradient Methods for Minimizing Composite Functions.” Math. Program. 140 (1, Ser. B):125–61. https://doi.org/10.1007/s10107-012-0629-5.

Paquette, C., H. Lin, D. Drusvyatskiy, J. Mairal, and Z. Harchaoui. 2017. “Catalyst Acceleration for Gradient-Based Non-Convex Optimization.” Preprint arXiv:1703.10993.

Polyak, B.T., and A.B. Juditsky. 1992. “Acceleration of Stochastic Approximation by Averaging.” SIAM J. Control Optim. 30 (4):838–55. https://doi.org/10.1137/0330046.

Rakhlin, A., O. Shamir, and K. Sridharan. 2012. “Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization.” In Proceedings of the 29th International Coference on International Conference on Machine Learning, 1571–8. ICML’12. USA: Omnipress. http://dl.acm.org/citation.cfm?id=3042573.3042774.

Robbins, H., and S. Monro. 1951. “A Stochastic Approximation Method.” Ann. Math. Statistics 22:400–407.

Schmidt, M., N. Le Roux, and F. Bach. 2013. “Minimizing Finite Sums with the Stochastic Average Gradient.” arXiv:1309.2388.

Shalev-Shwartz, S., and T. Zhang. 2012. “Proximal Stochastic Dual Coordinate Ascent.” arXiv:1211.2717.

S. Shalev-Shwartz and T. Zhang. 2015. “Accelerated Proximal Stochastic Dual Coordinate Ascent for Regularized Loss Minimization.” Mathematical Programming.

Singer, A. 2011. “Angular Synchronization by Eigenvectors and Semidefinite Programming.” Appl. Comput. Harmon. Anal. 30 (1):20–36. https://doi.org/10.1016/j.acha.2010.02.001.

Sun, J., Q. Qu, and J. Wright. 2017. “A Geometric Analysis of Phase Retrieval.” To Appear in Found. Comp. Math., arXiv:1602.06664.

Woodworth, B.E., and N. Srebro. 2016. “Tight Complexity Bounds for Optimizing Composite Objectives.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 3639–47. Curran Associates, Inc. http://papers.nips.cc/paper/6058-tight-complexity-bounds-for-optimizing-composite-objectives.pdf.

Wright, S.J. 1997. Primal-Dual Interior-Point Methods. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611971453.

Xiao, L., and T. Zhang. 2014. “A Proximal Stochastic Gradient Method with Progressive Variance Reduction.” SIAM J. Optim. 24 (4):2057–75. https://doi.org/10.1137/140961791.