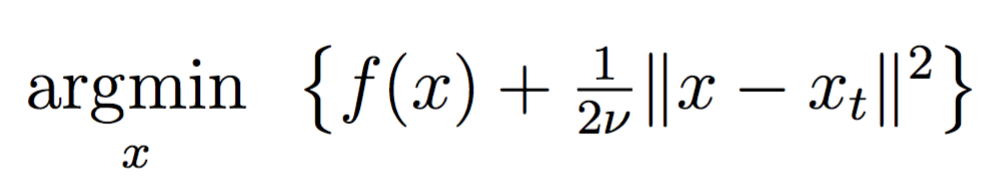This is episode 1 of the three part series that revisits the classical proximal point algorithm. See the previous post for introduction and notation.

The proximally guided subgradient method

As the first example of contemporary applications of the proximal point method, consider the problem of minimizing the expectation:¹

Here, \(\zeta\) is a random variable, and the only access to \(F\) is by sampling \(\zeta\). It is difficult to overstate the importance of this problem class (often called stochastic approximation) in large-scale optimization; see e.g. Bottou and Bousquet (2008); Bartlett, Jordan, and McAuliffe (2006).

When the problem is convex, the stochastic subgradient method (Polyak and Juditsky 1992; Robbins and Monro 1951; Nemirovski et al. 2008) has strong theoretical guarantees and is often the method of choice. In contrast, when applied to nonsmooth and nonconvex problems, the behavior of the method is poorly understood. The recent paper (Davis and Grimmer 2017) shows how to use the proximal point method to guide the subgradient iterates in this broader setting, with rigorous guarantees.

Henceforth, assume that the function \(x\mapsto f(x,\zeta)\) is \(\rho\)-weakly convex and \(L\)-Lipschitz for each \(\zeta\). Davis and Grimmer (2017) proposed the scheme outlined below.

Proximally guided stochastic subgradient method

• Data: \(x_0\in {\mathbb R}^d\), \(\{j_t\}\subset\mathbb{N}\), \(\{\alpha_j\}\subset{\mathbb R}_{++}\)
• For \(t=0,\ldots,T\) do
  • Set \(y_0=x_t\)
  • For \(j=0,\ldots,j_t-2\) do
    • Sample \(\zeta\) and choose \(v_j\in\partial (f(\cdot,\zeta)+\rho\|\cdot-x_t\|^2)(y_j)\)
    • Set \(y_{j+1}= y_j-\alpha_jv_j\)
  • Set \(x_{t+1}= \frac{1}{j_t}\sum_{j=0}^{j_t-1}y_j\)

The method proceeds by applying a proximal point method with each subproblem approximately solved by a stochastic subgradient method. The intuition is that each proximal subproblem is \(\rho/2\)-strongly convex and therefore according to well-known results (e.g. Lacoste-Julien, Schmidt, and Bach (2012); Rakhlin, Shamir, and Sridharan (2012); Hazan and Kale (2011); Juditsky and Nesterov (2014)), the stochastic subgradient method should converge at the rate \(O(\frac{1}{T})\) on the subproblem, in expectation. This intuition is not quite correct because the objective function of the subproblem is not globally Lipschitz – a key assumption for the \(O(\frac{1}{T})\) rate. Nonetheless, the authors show that warm-starting the subgradient method for each proximal subproblem with the current proximal iterate corrects this issue, yielding a favorable guarantees (Davis and Grimmer 2017 Theorem 1).

To describe the rate of convergence, set \(j_t=t+\lceil 648\log(648)\rceil\) and \(\alpha_j=\tfrac{2}{\rho(j+49)}\) in the Proximally guided stochastic subgradient method. Then the scheme will generate an iterate \(x\) satisfying

after at most

subgradient evaluations. This rate agrees with analogous guarantees for stochastic gradient methods for smooth nonconvex functions (Ghadimi and Lan 2013). It is also worth noting that convex constraints on \(x\) can be easily incorporated into the Proximally guided stochastic subgradient method by introducing a nearest-point projection in the definition of \(y_{j+1}\).

References

Abbe, E., A.S. Bandeira, A. Bracher, and A. Singer. 2014. “Decoding Binary Node Labels from Censored Edge Measurements: Phase Transition and Efficient Recovery.” IEEE Trans. Network Sci. Eng. 1 (1):10–22. https://doi.org/10.1109/TNSE.2014.2368716.

Agarwal, A., and L. Bottou. 2015. “A Lower Bound for the Optimization of Finite Sums.” In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6-11 July 2015, 78–86. http://leon.bottou.org/papers/agarwal-bottou-2015.

Allen-Zhu, Z. 2016. “Katyusha: The First Direct Acceleration of Stochastic Gradient Methods.” Preprint arXiv:1603.05953 (Version 5).

Arjevani, Y. 2017. “Limitations on Variance-Reduction and Acceleration Schemes for Finite Sums Optimization.” In Advances in Neural Information Processing Systems 30, edited by I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, 3543–52. Curran Associates, Inc. http://papers.nips.cc/paper/6945-limitations-on-variance-reduction-and-acceleration-schemes-for-finite-sums-optimization.pdf.

Bandeira, A.S., N. Boumal, and V. Voroninski. 2016. “On the Low-Rank Approach for Semidefinite Programs Arising in Synchronization and Community Detection.” In Proceedings of the 29th Conference on Learning Theory, COLT 2016, New York, Usa, June 23-26, 2016, 361–82. http://jmlr.org/proceedings/papers/v49/bandeira16.html.

Bartlett, P.L., M.I. Jordan, and J.D. McAuliffe. 2006. “Convexity, Classification, and Risk Bounds.” J. Amer. Statist. Assoc. 101 (473):138–56. https://doi-org.offcampus.lib.washington.edu/10.1198/016214505000000907.

Beck, A., and M. Teboulle. 2012. “Smoothing and First Order Methods: A Unified Framework.” SIAM J. Optim. 22 (2):557–80. https://doi.org/10.1137/100818327.

Bottou, L., and O. Bousquet. 2008. “The Tradeoffs of Large Scale Learning.” In Advances in Neural Information Processing Systems, 161–68. http://leon.bottou.org/publications/pdf/nips-2007.pdf.

Burke, J.V., and M.C. Ferris. 1995. “A Gauss-Newton Method for Convex Composite Optimization.” Math. Programming 71 (2, Ser. A):179–94. https://doi.org/10.1007/BF01585997.

Candès, E.J., X. Li, Y. Ma, and J. Wright. 2011. “Robust Principal Component Analysis?” J. ACM 58 (3):Art. 11, 37. https://doi.org/10.1145/1970392.1970395.

Candès, E.J., X. Li, and M. Soltanolkotabi. 2015. “Phase Retrieval via Wirtinger Flow: Theory and Algorithms.” IEEE Trans. Inform. Theory 61 (4):1985–2007. https://doi.org/10.1109/TIT.2015.2399924.

Carmon, Y., J.C. Duchi, O. Hinder, and A. Sidford. 2017a. “‘Convex Until Proven Guilty’: Dimension-Free Acceleration of Gradient Descent on Non-Convex Functions.” In Proceedings of the 34th International Conference on Machine Learning, 70:654–63.

Y. Carmon, J.C. Duchi, O. Hinder, and A. Sidford. Lower bounds for finding stationary points I. Preprint arXiv:1710.11606.

Cartis, C., N.I.M. Gould, and P.L. Toint. 2011. “On the Evaluation Complexity of Composite Function Minimization with Applications to Nonconvex Nonlinear Programming.” SIAM J. Optim. 21 (4):1721–39. https://doi.org/10.1137/11082381X.

Chambolle, A., and T. Pock. 2011. “A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging.” J. Math. Imaging Vision 40 (1):120–45. https://doi.org/10.1007/s10851-010-0251-1.

Chandrasekaran, V., S. Sanghavi, P. A. Parrilo, and A.S. Willsky. 2011. “Rank-Sparsity Incoherence for Matrix Decomposition.” SIAM J. Optim. 21 (2):572–96. https://doi.org/10.1137/090761793.

Chen, Y., and E.J. Candès. 2017. “Solving Random Quadratic Systems of Equations Is Nearly as Easy as Solving Linear Systems.” Comm. Pure Appl. Math. 70 (5):822–83. https://doi-org.offcampus.lib.washington.edu/10.1002/cpa.21638.

Davis, D. 2016. “SMART: The Stochastic Monotone Aggregated Root-Finding Algorithm.” Preprint arXiv:1601.00698.

Davis, D., D. Drusvyatskiy, and C. Paquette. 2017. “The Nonsmooth Landscape of Phase Retrieval.” Preprint arXiv:1711.03247.

Davis, D., and B. Grimmer. 2017. “Proximally Guided Stochastic Sbgradient Method for Nonsmooth, Nonconvex Problems.” Preprint, arXiv:1707.03505.

Defazio, A. 2016. “A Simple Practical Accelerated Method for Finite Sums.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 676–84. Curran Associates, Inc. http://papers.nips.cc/paper/6154-a-simple-practical-accelerated-method-for-finite-sums.pdf.

Defazio, A., F. Bach, and S. Lacoste-Julien. 2014. “SAGA: A Fast Incremental Gradient Method with Support for Non-Strongly Convex Composite Objectives.” In Advances in Neural Information Processing Systems 27, edited by Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger, 1646–54. Curran Associates, Inc.

Defazio, A., J. Domke, and T.S. Caetano. 2014. “Finito: A Faster, Permutable Incremental Gradient Method for Big Data Problems.” In ICML, 1125–33.

Drusvyatskiy, D., and A.S. Lewis. 2013. “Tilt Stability, Uniform Quadratic Growth, and Strong Metric Regularity of the Subdifferential.” SIAM J. Optim. 23 (1):256–67. https://doi.org/10.1137/120876551.

D. Drusvyatskiy and A.S. Lewis. 2016. “Error Bounds, Quadratic Growth, and Linear Convergence of Proximal Methods.” To Appear in Math. Oper. Res., arXiv:1602.06661.

Drusvyatskiy, D., B.S. Mordukhovich, and T.T.A. Nghia. 2014. “Second-Order Growth, Tilt-Stability, and Metric Regularity of the Subdifferential.” J. Convex Anal. 21 (4):1165–92.

Drusvyatskiy, D., and C. Paquette. 2016. “Efficiency of Minimizing Compositions of Convex Functions and Smooth Maps.” Preprint, arXiv:1605.00125.

Duchi, J.C., and F. Ruan. 2017a. “Solving (Most) of a Set of Quadratic Equalities: Composite Optimization for Robust Phase Retrieval.” Preprint arXiv:1705.02356.

J.C. Duchi and F. Ruan. 2017b. “Stochastic Methods for Composite Optimization Problems.” Preprint arXiv:1703.08570.

Eldar, Y.C., and S. Mendelson. 2014. “Phase Retrieval: Stability and Recovery Guarantees.” Appl. Comput. Harmon. Anal. 36 (3):473–94. https://doi.org/10.1016/j.acha.2013.08.003.

Frostig, R., R. Ge, S.M. Kakade, and A. Sidford. 2015. “Un-Regularizing: Approximate Proximal Point and Faster Stochastic Algorithms for Empirical Risk Minimization.” In Proceedings of the 32nd International Conference on Machine Learning (ICML).

Ghadimi, S., and G. Lan. 2013. “Stochastic First- and Zeroth-Order Methods for Nonconvex Stochastic Programming.” SIAM J. Optim. 23 (4):2341–68. https://doi.org/10.1137/120880811.

Güler, O. 1992. “New Proximal Point Algorithms for Convex Minimization.” SIAM J. Optim. 2 (4):649–64. https://doi-org.offcampus.lib.washington.edu/10.1137/0802032.

Hazan, E., and S. Kale. 2011. “Beyond the Regret Minimization Barrier: An Optimal Algorithm for Stochastic Strongly-Convex Optimization.” In Proceedings of the 24th Annual Conference on Learning Theory, edited by Sham M. Kakade and Ulrike von Luxburg, 19:421–36. Proceedings of Machine Learning Research. Budapest, Hungary: PMLR.

Johnson, R., and T. Zhang. 2013. “Accelerating Stochastic Gradient Descent Using Predictive Variance Reduction.” In Proceedings of the 26th International Conference on Neural Information Processing Systems, 315–23. NIPS’13. USA: Curran Associates Inc. http://dl.acm.org/citation.cfm?id=2999611.2999647.

Juditsky, A., and Y. Nesterov. 2014. “Deterministic and Stochastic Primal-Dual Subgradient Algorithms for Uniformly Convex Minimization.” Stoch. Syst. 4 (1):44–80. https://doi-org.offcampus.lib.washington.edu/10.1214/10-SSY010.

Lacoste-Julien, S., M. Schmidt, and F. Bach. 2012. “A Simpler Approach to Obtaining an \({O}(1/t)\) Convergence Rate for the Projected Stochastic Subgradient Method.” Arxiv arXiv:1212.2002.

Lan, G. 2015. “An Optimal Randomized Incremental Gradient Method.” arXiv:1507.02000.

Lemarechal, C., J.-J. Strodiot, and A. Bihain. 1981. “On a Bundle Algorithm for Nonsmooth Optimization.” In Nonlinear Programming, 4 (Madison, Wis., 1980), 245–82. Academic Press, New York-London.

Lewis, A.S., and S.J. Wright. 2015. “A Proximal Method for Composite Minimization.” Math. Program. Springer Berlin Heidelberg, 1–46. https://doi.org/10.1007/s10107-015-0943-9.

Lin, H., J. Mairal, and Z. Harchaoui. 2015. “A Universal Catalyst for First-Order Optimization.” In Advances in Neural Information Processing Systems, 3366–74.

Luke, R. 2017. “Phase Retrieval, What’s New?” SIAG/OPT Views and News 25 (1).

Mairal, J. 2015. “Incremental Majorization-Minimization Optimization with Application to Large-Scale Machine Learning.” SIAM Journal on Optimization 25 (2):829–55.

Nemirovski, A. 2004. “Prox-Method with Rate of Convergence \(O(1/t)\) for Variational Inequalities with Lipschitz Continuous Monotone Operators and Smooth Convex-Concave Saddle Point Problems.” SIAM J. Optim. 15 (1):229–51. https://doi.org/10.1137/S1052623403425629.

Nemirovski, A., A. Juditsky, G. Lan, and A. Shapiro. 2008. “Robust Stochastic Approximation Approach to Stochastic Programming.” SIAM J. Optim. 19 (4):1574–1609. https://doi-org.offcampus.lib.washington.edu/10.1137/070704277.

Nemirovsky, A.S., and D.B. Yudin. 1983. Problem Complexity and Method Efficiency in Optimization. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York.

Nesterov, Y., and A. Nemirovskii. 1994. Interior-Point Polynomial Algorithms in Convex Programming. Vol. 13. SIAM Studies in Applied Mathematics. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611970791.

Nesterov, Yu. 1983. “A Method for Solving the Convex Programming Problem with Convergence Rate \(O(1/k^{2})\).” Dokl. Akad. Nauk SSSR 269 (3):543–47.

Nesterov, Yu. 2005. “Smooth Minimization of Non-Smooth Functions.” Math. Program. 103 (1, Ser. A):127–52. https://doi.org/10.1007/s10107-004-0552-5.

Nesterov, Yu. 2007. “Modified Gauss-Newton Scheme with Worst Case Guarantees for Global Performance.” Optim. Methods Softw. 22 (3):469–83. https://doi.org/10.1080/08927020600643812.

Nesterov, Yu. 2013. “Gradient Methods for Minimizing Composite Functions.” Math. Program. 140 (1, Ser. B):125–61. https://doi.org/10.1007/s10107-012-0629-5.

Paquette, C., H. Lin, D. Drusvyatskiy, J. Mairal, and Z. Harchaoui. 2017. “Catalyst Acceleration for Gradient-Based Non-Convex Optimization.” Preprint arXiv:1703.10993.

Polyak, B.T., and A.B. Juditsky. 1992. “Acceleration of Stochastic Approximation by Averaging.” SIAM J. Control Optim. 30 (4):838–55. https://doi.org/10.1137/0330046.

Rakhlin, A., O. Shamir, and K. Sridharan. 2012. “Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization.” In Proceedings of the 29th International Coference on International Conference on Machine Learning, 1571–8. ICML’12. USA: Omnipress. http://dl.acm.org/citation.cfm?id=3042573.3042774.

Robbins, H., and S. Monro. 1951. “A Stochastic Approximation Method.” Ann. Math. Statistics 22:400–407.

Schmidt, M., N. Le Roux, and F. Bach. 2013. “Minimizing Finite Sums with the Stochastic Average Gradient.” arXiv:1309.2388.

Shalev-Shwartz, S., and T. Zhang. 2012. “Proximal Stochastic Dual Coordinate Ascent.” arXiv:1211.2717.

S. Shalev-Shwartz and T. Zhang. 2015. “Accelerated Proximal Stochastic Dual Coordinate Ascent for Regularized Loss Minimization.” Mathematical Programming.

Singer, A. 2011. “Angular Synchronization by Eigenvectors and Semidefinite Programming.” Appl. Comput. Harmon. Anal. 30 (1):20–36. https://doi.org/10.1016/j.acha.2010.02.001.

Sun, J., Q. Qu, and J. Wright. 2017. “A Geometric Analysis of Phase Retrieval.” To Appear in Found. Comp. Math., arXiv:1602.06664.

Woodworth, B.E., and N. Srebro. 2016. “Tight Complexity Bounds for Optimizing Composite Objectives.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 3639–47. Curran Associates, Inc. http://papers.nips.cc/paper/6058-tight-complexity-bounds-for-optimizing-composite-objectives.pdf.

Wright, S.J. 1997. Primal-Dual Interior-Point Methods. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611971453.

Xiao, L., and T. Zhang. 2014. “A Proximal Stochastic Gradient Method with Progressive Variance Reduction.” SIAM J. Optim. 24 (4):2057–75. https://doi.org/10.1137/140961791.