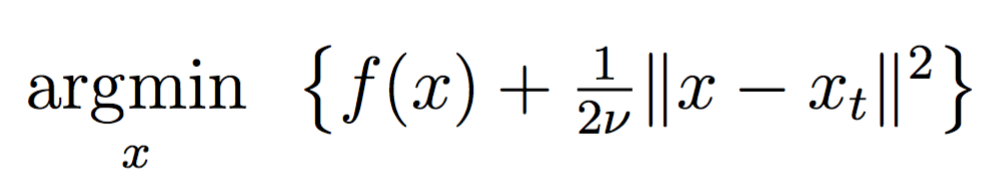This is episode 2 of the three-part series that revisits the classical proximal point algorithm. See the first post on this topic for an introduction and notation.

The prox-linear algorithm

For well-structured weakly convex problems, one can hope for faster numerical methods than the subgradient scheme. In this episode, I will focus on the composite problem class \(\mathcal{C}\). To simplify the exposition, I will assume \(L=1\), which can always be arranged by rescaling.

Since composite functions are weakly convex, one could apply the proximal point method directly, while setting the parameter \(\nu\leq\beta^{-1}\). Even though the proximal subproblems are strongly convex, they are not in a form that is most amenable to convex optimization techniques. Indeed, most convex optimization algorithms are designed for minimizing a sum of a convex function and a composition of a convex function with a linear map. This observation suggests introducing the following modification to the proximal-point algorithm. Given a current iterate \(x_t\), the prox-linear method sets

where \(F(x;y)\) is the local convex model

In other words, each proximal subproblem is approximated by linearizing the smooth map \(c\) at the current iterate \(x_t\).

The main advantage is that each subproblem is now a sum of a strongly convex function and a composition of a Lipschitz convex function with a linear map. A variety of methods utilizing this structure can be formally applied; e.g. smoothing (Nesterov 2005), saddle-point (Nemirovski 2004; Chambolle and Pock 2011), and interior point algorithms (Nesterov and Nemirovskii 1994; Wright 1997). Which of these methods is practical depends on the specifics of the problem, such as the size and the cost of vector-matrix multiplications.

It is instructive to note that in the simplest setting of additive composite problems (Example 1), the prox-linear method reduces to the popular proximal-gradient algorithm or ISTA (Beck and Teboulle 2012). For nonlinear least squares, the prox-linear method is a close variant of Gauss-Newton.

Recall that the step-size of the proximal point method provides a convenient stopping criteria, since it directly relates to the gradient of the Moreau envelope – a smooth approximation of the objective function. Is there such an interpretation for the prox-linear method? This question is central, since termination criteria is not only used to stop the method but also to judge its efficiency and to compare against competing methods.

The answer is yes. Even though one can not evaluate the gradient \(\|\nabla F_{\frac{1}{2\beta}}\|\) directly, the scaled step-size of the prox-linear method

is a good surrogate (Drusvyatskiy and Paquette 2016 Theorem 4.5):

In particular, the prox-linear method will find a point \(x\) satisfying \(\|\nabla F_{\frac{1}{2\beta}}(x)\|^2\leq\varepsilon\) after at most \(O\left(\frac{\beta(F(x_0)-\inf F)}{\varepsilon}\right)\) iterations. In the simplest setting when \(g=0\) and \(h(t)=t\), this rate reduces to the well-known convergence guarantee of gradient descent, which is black-box optimal for \(C^1\)-smooth nonconvex optimization (Carmon et al. 2017b).

It is worthwhile to note that a number of improvements to the basic prox-linear method were recently proposed. Cartis, Gould, and Toint (2011) discuss trust region variants and their complexity guarantees, while Duchi and Ruan (2017b) propose stochastic extensions of the scheme and prove almost sure convergence. Drusvyatskiy and Paquette (2016) discuss overall complexity guarantees when the convex subproblems can only be solved by first-order methods, and proposes an inertial variant of the scheme whose convergence guarantees automatically adapt to the near-convexity of the problem.

Local rapid convergence

Under typical regularity conditions, the prox-linear method exhibits the same types of rapid convergence guarantees as the proximal point method. I will illustrate with two intuitive and widely used regularity conditions, yielding local linear and quadratic convergence, respectively.

A local minimizer \(\bar x\) of \(F\) is \(\alpha\)-tilt-stable if there exists \(r>0\) such that the solution map

is \(1/\alpha\)-Lipschitz around \(0\) with \(M(0)=\bar x\).

This condition might seem unfamiliar to convex optimization specialist. Though not obvious, tilt-stability is equivalent to a uniform quadratic growth property and a subtle localization of strong convexity of \(F\). See Drusvyatskiy and Lewis (2013) or Drusvyatskiy, Mordukhovich, and Nghia (2014) for more details on these equivalences. Under the tilt-stability assumption, the prox-linear method initialized sufficiently close to \(\bar x\) produces iterates that converge at a linear rate \(1-\alpha/\beta\).

The second regularity condition models sharp growth of the function around the minimizer. Let \(S\) be the set of all stationary points of \(F\), meaning \(x\) lies in \(S\) if and only if the directional derivative \(F'(x;v)\) is nonnegative in every direction \(v\in {\mathbb R}^d\).

A local minimizer \(\bar x\) of \(F\) is sharp if there exists \(\alpha>0\) and a neighborhood \(\mathcal{X}\) of \(\bar x\) such that

Under the sharpness condition, the prox-linear method initialized sufficiently close to \(\bar x\) produces iterates that converge quadratically.

For well-structured problems, one can hope to justify the two regularity conditions above under statistical assumptions. The recent work of Duchi and Ruan (2017a) on the phase retrieval problem is an interesting recent example. Under mild statistical assumptions on the data generating mechanism, sharpness is assured with high probability. Therefore the prox-linear method (and even subgradient methods (Davis, Drusvyatskiy, and Paquette 2017)) converge rapidly, when initialized within a constant relative distance of an optimal solution.

References

Abbe, E., A.S. Bandeira, A. Bracher, and A. Singer. 2014. “Decoding Binary Node Labels from Censored Edge Measurements: Phase Transition and Efficient Recovery.” IEEE Trans. Network Sci. Eng. 1 (1):10–22. https://doi.org/10.1109/TNSE.2014.2368716.

Agarwal, A., and L. Bottou. 2015. “A Lower Bound for the Optimization of Finite Sums.” In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6-11 July 2015, 78–86. http://leon.bottou.org/papers/agarwal-bottou-2015.

Allen-Zhu, Z. 2016. “Katyusha: The First Direct Acceleration of Stochastic Gradient Methods.” Preprint arXiv:1603.05953 (Version 5).

Arjevani, Y. 2017. “Limitations on Variance-Reduction and Acceleration Schemes for Finite Sums Optimization.” In Advances in Neural Information Processing Systems 30, edited by I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, 3543–52. Curran Associates, Inc. http://papers.nips.cc/paper/6945-limitations-on-variance-reduction-and-acceleration-schemes-for-finite-sums-optimization.pdf.

Bandeira, A.S., N. Boumal, and V. Voroninski. 2016. “On the Low-Rank Approach for Semidefinite Programs Arising in Synchronization and Community Detection.” In Proceedings of the 29th Conference on Learning Theory, COLT 2016, New York, Usa, June 23-26, 2016, 361–82. http://jmlr.org/proceedings/papers/v49/bandeira16.html.

Bartlett, P.L., M.I. Jordan, and J.D. McAuliffe. 2006. “Convexity, Classification, and Risk Bounds.” J. Amer. Statist. Assoc. 101 (473):138–56. https://doi-org.offcampus.lib.washington.edu/10.1198/016214505000000907.

Beck, A., and M. Teboulle. 2012. “Smoothing and First Order Methods: A Unified Framework.” SIAM J. Optim. 22 (2):557–80. https://doi.org/10.1137/100818327.

Bottou, L., and O. Bousquet. 2008. “The Tradeoffs of Large Scale Learning.” In Advances in Neural Information Processing Systems, 161–68. http://leon.bottou.org/publications/pdf/nips-2007.pdf.

Burke, J.V., and M.C. Ferris. 1995. “A Gauss-Newton Method for Convex Composite Optimization.” Math. Programming 71 (2, Ser. A):179–94. https://doi.org/10.1007/BF01585997.

Candès, E.J., X. Li, Y. Ma, and J. Wright. 2011. “Robust Principal Component Analysis?” J. ACM 58 (3):Art. 11, 37. https://doi.org/10.1145/1970392.1970395.

Candès, E.J., X. Li, and M. Soltanolkotabi. 2015. “Phase Retrieval via Wirtinger Flow: Theory and Algorithms.” IEEE Trans. Inform. Theory 61 (4):1985–2007. https://doi.org/10.1109/TIT.2015.2399924.

Carmon, Y., J.C. Duchi, O. Hinder, and A. Sidford. 2017a. “‘Convex Until Proven Guilty’: Dimension-Free Acceleration of Gradient Descent on Non-Convex Functions.” In Proceedings of the 34th International Conference on Machine Learning, 70:654–63.

Y. Carmon, J.C. Duchi, O. Hinder, and A. Sidford. Lower bounds for finding stationary points I. Preprint arXiv:1710.11606.

Cartis, C., N.I.M. Gould, and P.L. Toint. 2011. “On the Evaluation Complexity of Composite Function Minimization with Applications to Nonconvex Nonlinear Programming.” SIAM J. Optim. 21 (4):1721–39. https://doi.org/10.1137/11082381X.

Chambolle, A., and T. Pock. 2011. “A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging.” J. Math. Imaging Vision 40 (1):120–45. https://doi.org/10.1007/s10851-010-0251-1.

Chandrasekaran, V., S. Sanghavi, P. A. Parrilo, and A.S. Willsky. 2011. “Rank-Sparsity Incoherence for Matrix Decomposition.” SIAM J. Optim. 21 (2):572–96. https://doi.org/10.1137/090761793.

Chen, Y., and E.J. Candès. 2017. “Solving Random Quadratic Systems of Equations Is Nearly as Easy as Solving Linear Systems.” Comm. Pure Appl. Math. 70 (5):822–83. https://doi-org.offcampus.lib.washington.edu/10.1002/cpa.21638.

Davis, D. 2016. “SMART: The Stochastic Monotone Aggregated Root-Finding Algorithm.” Preprint arXiv:1601.00698.

Davis, D., D. Drusvyatskiy, and C. Paquette. 2017. “The Nonsmooth Landscape of Phase Retrieval.” Preprint arXiv:1711.03247.

Davis, D., and B. Grimmer. 2017. “Proximally Guided Stochastic Sbgradient Method for Nonsmooth, Nonconvex Problems.” Preprint, arXiv:1707.03505.

Defazio, A. 2016. “A Simple Practical Accelerated Method for Finite Sums.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 676–84. Curran Associates, Inc. http://papers.nips.cc/paper/6154-a-simple-practical-accelerated-method-for-finite-sums.pdf.

Defazio, A., F. Bach, and S. Lacoste-Julien. 2014. “SAGA: A Fast Incremental Gradient Method with Support for Non-Strongly Convex Composite Objectives.” In Advances in Neural Information Processing Systems 27, edited by Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger, 1646–54. Curran Associates, Inc.

Defazio, A., J. Domke, and T.S. Caetano. 2014. “Finito: A Faster, Permutable Incremental Gradient Method for Big Data Problems.” In ICML, 1125–33.

Drusvyatskiy, D., and A.S. Lewis. 2013. “Tilt Stability, Uniform Quadratic Growth, and Strong Metric Regularity of the Subdifferential.” SIAM J. Optim. 23 (1):256–67. https://doi.org/10.1137/120876551.

D. Drusvyatskiy and A.S. Lewis. 2016. “Error Bounds, Quadratic Growth, and Linear Convergence of Proximal Methods.” To Appear in Math. Oper. Res., arXiv:1602.06661.

Drusvyatskiy, D., B.S. Mordukhovich, and T.T.A. Nghia. 2014. “Second-Order Growth, Tilt-Stability, and Metric Regularity of the Subdifferential.” J. Convex Anal. 21 (4):1165–92.

Drusvyatskiy, D., and C. Paquette. 2016. “Efficiency of Minimizing Compositions of Convex Functions and Smooth Maps.” Preprint, arXiv:1605.00125.

Duchi, J.C., and F. Ruan. 2017a. “Solving (Most) of a Set of Quadratic Equalities: Composite Optimization for Robust Phase Retrieval.” Preprint arXiv:1705.02356.

J.C. Duchi and F. Ruan. 2017b. “Stochastic Methods for Composite Optimization Problems.” Preprint arXiv:1703.08570.

Eldar, Y.C., and S. Mendelson. 2014. “Phase Retrieval: Stability and Recovery Guarantees.” Appl. Comput. Harmon. Anal. 36 (3):473–94. https://doi.org/10.1016/j.acha.2013.08.003.

Frostig, R., R. Ge, S.M. Kakade, and A. Sidford. 2015. “Un-Regularizing: Approximate Proximal Point and Faster Stochastic Algorithms for Empirical Risk Minimization.” In Proceedings of the 32nd International Conference on Machine Learning (ICML).

Ghadimi, S., and G. Lan. 2013. “Stochastic First- and Zeroth-Order Methods for Nonconvex Stochastic Programming.” SIAM J. Optim. 23 (4):2341–68. https://doi.org/10.1137/120880811.

Güler, O. 1992. “New Proximal Point Algorithms for Convex Minimization.” SIAM J. Optim. 2 (4):649–64. https://doi-org.offcampus.lib.washington.edu/10.1137/0802032.

Hazan, E., and S. Kale. 2011. “Beyond the Regret Minimization Barrier: An Optimal Algorithm for Stochastic Strongly-Convex Optimization.” In Proceedings of the 24th Annual Conference on Learning Theory, edited by Sham M. Kakade and Ulrike von Luxburg, 19:421–36. Proceedings of Machine Learning Research. Budapest, Hungary: PMLR.

Johnson, R., and T. Zhang. 2013. “Accelerating Stochastic Gradient Descent Using Predictive Variance Reduction.” In Proceedings of the 26th International Conference on Neural Information Processing Systems, 315–23. NIPS’13. USA: Curran Associates Inc. http://dl.acm.org/citation.cfm?id=2999611.2999647.

Juditsky, A., and Y. Nesterov. 2014. “Deterministic and Stochastic Primal-Dual Subgradient Algorithms for Uniformly Convex Minimization.” Stoch. Syst. 4 (1):44–80. https://doi-org.offcampus.lib.washington.edu/10.1214/10-SSY010.

Lacoste-Julien, S., M. Schmidt, and F. Bach. 2012. “A Simpler Approach to Obtaining an \({O}(1/t)\) Convergence Rate for the Projected Stochastic Subgradient Method.” Arxiv arXiv:1212.2002.

Lan, G. 2015. “An Optimal Randomized Incremental Gradient Method.” arXiv:1507.02000.

Lemarechal, C., J.-J. Strodiot, and A. Bihain. 1981. “On a Bundle Algorithm for Nonsmooth Optimization.” In Nonlinear Programming, 4 (Madison, Wis., 1980), 245–82. Academic Press, New York-London.

Lewis, A.S., and S.J. Wright. 2015. “A Proximal Method for Composite Minimization.” Math. Program. Springer Berlin Heidelberg, 1–46. https://doi.org/10.1007/s10107-015-0943-9.

Lin, H., J. Mairal, and Z. Harchaoui. 2015. “A Universal Catalyst for First-Order Optimization.” In Advances in Neural Information Processing Systems, 3366–74.

Luke, R. 2017. “Phase Retrieval, What’s New?” SIAG/OPT Views and News 25 (1).

Mairal, J. 2015. “Incremental Majorization-Minimization Optimization with Application to Large-Scale Machine Learning.” SIAM Journal on Optimization 25 (2):829–55.

Nemirovski, A. 2004. “Prox-Method with Rate of Convergence \(O(1/t)\) for Variational Inequalities with Lipschitz Continuous Monotone Operators and Smooth Convex-Concave Saddle Point Problems.” SIAM J. Optim. 15 (1):229–51. https://doi.org/10.1137/S1052623403425629.

Nemirovski, A., A. Juditsky, G. Lan, and A. Shapiro. 2008. “Robust Stochastic Approximation Approach to Stochastic Programming.” SIAM J. Optim. 19 (4):1574–1609. https://doi-org.offcampus.lib.washington.edu/10.1137/070704277.

Nemirovsky, A.S., and D.B. Yudin. 1983. Problem Complexity and Method Efficiency in Optimization. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York.

Nesterov, Y., and A. Nemirovskii. 1994. Interior-Point Polynomial Algorithms in Convex Programming. Vol. 13. SIAM Studies in Applied Mathematics. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611970791.

Nesterov, Yu. 1983. “A Method for Solving the Convex Programming Problem with Convergence Rate \(O(1/k^{2})\).” Dokl. Akad. Nauk SSSR 269 (3):543–47.

Nesterov, Yu. 2005. “Smooth Minimization of Non-Smooth Functions.” Math. Program. 103 (1, Ser. A):127–52. https://doi.org/10.1007/s10107-004-0552-5.

Nesterov, Yu. 2007. “Modified Gauss-Newton Scheme with Worst Case Guarantees for Global Performance.” Optim. Methods Softw. 22 (3):469–83. https://doi.org/10.1080/08927020600643812.

Nesterov, Yu. 2013. “Gradient Methods for Minimizing Composite Functions.” Math. Program. 140 (1, Ser. B):125–61. https://doi.org/10.1007/s10107-012-0629-5.

Paquette, C., H. Lin, D. Drusvyatskiy, J. Mairal, and Z. Harchaoui. 2017. “Catalyst Acceleration for Gradient-Based Non-Convex Optimization.” Preprint arXiv:1703.10993.

Polyak, B.T., and A.B. Juditsky. 1992. “Acceleration of Stochastic Approximation by Averaging.” SIAM J. Control Optim. 30 (4):838–55. https://doi.org/10.1137/0330046.

Rakhlin, A., O. Shamir, and K. Sridharan. 2012. “Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization.” In Proceedings of the 29th International Coference on International Conference on Machine Learning, 1571–8. ICML’12. USA: Omnipress. http://dl.acm.org/citation.cfm?id=3042573.3042774.

Robbins, H., and S. Monro. 1951. “A Stochastic Approximation Method.” Ann. Math. Statistics 22:400–407.

Schmidt, M., N. Le Roux, and F. Bach. 2013. “Minimizing Finite Sums with the Stochastic Average Gradient.” arXiv:1309.2388.

Shalev-Shwartz, S., and T. Zhang. 2012. “Proximal Stochastic Dual Coordinate Ascent.” arXiv:1211.2717.

S. Shalev-Shwartz and T. Zhang. 2015. “Accelerated Proximal Stochastic Dual Coordinate Ascent for Regularized Loss Minimization.” Mathematical Programming.

Singer, A. 2011. “Angular Synchronization by Eigenvectors and Semidefinite Programming.” Appl. Comput. Harmon. Anal. 30 (1):20–36. https://doi.org/10.1016/j.acha.2010.02.001.

Sun, J., Q. Qu, and J. Wright. 2017. “A Geometric Analysis of Phase Retrieval.” To Appear in Found. Comp. Math., arXiv:1602.06664.

Woodworth, B.E., and N. Srebro. 2016. “Tight Complexity Bounds for Optimizing Composite Objectives.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 3639–47. Curran Associates, Inc. http://papers.nips.cc/paper/6058-tight-complexity-bounds-for-optimizing-composite-objectives.pdf.

Wright, S.J. 1997. Primal-Dual Interior-Point Methods. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611971453.

Xiao, L., and T. Zhang. 2014. “A Proximal Stochastic Gradient Method with Progressive Variance Reduction.” SIAM J. Optim. 24 (4):2057–75. https://doi.org/10.1137/140961791.