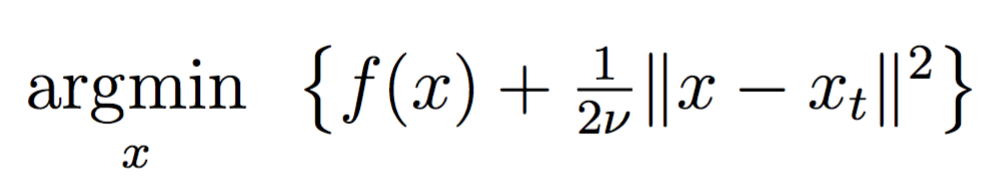This is episode 3 of the three part series that revisits the classical proximal point algorithm. See the first post on the subject for introduction and notation.

Catalyst acceleration

In the previous posts, we looked at the proximally guided subgradient method and the prox-linear algorithm. The final example concerns inertial acceleration in convex optimization. Setting the groundwork, consider a \(\mu\)-strongly convex function \(f\) with a \(\beta\)-Lipschitz gradient map \(x\mapsto \nabla f(x)\). Classically, gradient descent will find a point \(x\) satisfying \(f(x)-\min f<\varepsilon\) after at most

iterations. Accelerated gradient methods, beginning with Nesterov (1983), equip the gradient descent method with an inertial correction. Such methods have the much lower complexity guarantee

which is optimal within the first-order oracle model of computation (Nemirovsky and Yudin 1983).

It is natural to ask which other methods, aside from gradient descent, can be “accelerated”. For example, one may wish to accelerate coordinate descent or so-called variance reduced methods for finite sum problems; I will comment on the latter problem class shortly.

One appealing strategy relies on the proximal point method. Güler (1992) showed that the proximal point method itself can be equipped with inertial steps leading to improved convergence guarantees. Building on this work, Lin, Mairal, and Harchaoui (2015; 2017) explained how to derive the total complexity guarantees for an inexact accelerated proximal point method that take into account the cost of applying an arbitrary linearly convergent algorithm \(\mathcal{M}\) to the subproblems. Their Catalyst acceleration framework is summarized below. The code for Catalyst is publicly available here.

Catalyst Acceleration

• Data: \(x_0\in {\mathbb R}^d\), \(\kappa>0\), algorithm \(\mathcal{M}\)

• Set \(q= \mu/(\mu+\kappa)\), \(\alpha_0=\sqrt{q}\), and \(y_0=x_0\)

• For \(t=0,\ldots,T\) do

  • Use \(\mathcal{M}\) to approximately solve:

    \[x_t\approx \underset{x \in {\mathbb R}^d}{\operatorname{argmin}} \left\{F(x)+\frac{\kappa}{2}\|x-y_{t-1}\|^2\right\}.\;\]

  • Compute \(\alpha_t\in (0,1)\) from the equation

    \[\alpha_t^2=(1-\alpha_t)\alpha_{t-1}^2+q\alpha_t.\;\]

  • Compute:

    \[\begin{aligned} \beta_t&=\frac{\alpha_{t-1}(1-\alpha_{t-1})}{\alpha_{t-1}^2+\alpha_t},\\ y_t&=x_t+\beta_t(x_t-x_{t-1}). \end{aligned}\]

To state the guarantees of this method, suppose that \(\mathcal{M}\) converges on the proximal subproblem in function value at a linear rate \(1-\tau\in (0,1)\). Then a simple termination policy on the subproblems to solve for \(x_t\) yields an algorithm with overall complexity

That is, the expression above describes the maximal number of iterations of \(\mathcal{M}\) used by the Catalyst algorithm until it finds a point \(x\) satisfying \(f(x)-\inf f\leq \varepsilon\). Typically \(\tau\) depends on \(\kappa\); therefore the best choice of \(\kappa\) is the one that minimizes the ratio \(\frac{\sqrt{\mu+\kappa}}{\tau \sqrt{\mu}}\).

The main motivation for the Catalyst framework, and its most potent application, is the regularized Empirical Risk Minimization (ERM) problem:

Such large-finite sum problems are ubiquitous in machine learning and high-dimensional statistics, where each function \(f_i\) typically models a misfit between predicted and observed data while \(g\) promotes some low dimensional structure on \(x\), such as sparsity or low-rank.

Assume that \(f\) is \(\mu\)-strongly convex and each individual \(f_i\) is \(C^1\)-smooth with \(\beta\)-Lipschitz gradient. Since \(m\) is assumed to be huge, the complexity of numerical methods is best measured in terms of the total number of individual gradient evaluations \(\nabla f_i\). In particular, fast gradient methods have the worst-case complexity

since each iteration requires evaluation of all the individual gradients \(\{\nabla f_i(x)\}_{i=1}^m\). Variance reduced algorithms, such as SAG (Schmidt, Roux, and Bach 2013), SAGA (Defazio, Bach, and Lacoste-Julien 2014), SDCA (Shalev-Shwartz and Zhang 2012), SMART (Davis 2016), SVRG (Johnson and Zhang 2013; Xiao and Zhang 2014), FINITO (Defazio, Domke, and Caetano 2014), and MISO (Mairal 2015; Lin, Mairal, and Harchaoui 2015), aim to improve the dependence on \(m\). In their raw form, all of these methods exhibit a similar complexity

in expectation, and differ only in storage requirements and in whether one needs to know explicitly the strong convexity constant.

It was a long standing open question to determine if the dependence on \(\beta/\mu\) can be improved. This is not quite possible in full generality, and instead one should expect a rate of the form

Indeed, such a rate would be optimal in an appropriate oracle model of complexity (Woodworth and Srebro 2016; Arjevani 2017; Agarwal and Bottou 2015; Lan 2015). Thus acceleration for ERM problems is only beneficial in the setting \(m< \beta/\mu\).

Early examples for specific algorithms are the accelerated SDCA (Shalev-Shwartz and Zhang 2015), APPA (Frostig et al. 2015), and RPDG (Lan 2015).¹ The accelerated SDCA and APPA, in particular, use a specialized proximal-point construction.² Catalyst generic acceleration allows to accelerate all of the variance reduced methods above in a single conceptually transparent framework. It is worth noting that the first direct accelerated variance reduced methods for ERM problems were recently proposed in Allen-Zhu (2016) and Defazio (2016).

In contrast to the convex setting, the role of inertia for nonconvex problems is not nearly as well understood. In particular, gradient descent is black-box optimal for \(C^1\)-smooth nonconvex minimization (Carmon et al. 2017b), and therefore inertia can not help in the worst case. On the other hand, the recent paper (Carmon et al. 2017a) presents a first-order method for minimizing \(C^2\) and \(C^3\) smooth functions that is provably faster than gradient descent. At its core, their algorithm also combines inertia with the proximal point method. For a partial extension of the Catalyst framework to weakly convex problems, see Paquette et al. (2017).

Conclusion

The proximal point method has long been ingrained in the foundations of optimization. Recent progress in large scale computing has shown that the proximal point method is not only conceptual, but can guide methodology. Though direct methods are usually preferable, proximally guided algorithms can be equally effective and often lead to more easily interpretable numerical methods. In this blog, I outlined three examples of this viewpoint, where the proximal-point method guides both the design and analysis of numerical methods.

Acknowledgements

The author thanks Damek Davis, John Duchi, and Zaid Harchaoui for their helpful comments on an early draft.

References

Abbe, E., A.S. Bandeira, A. Bracher, and A. Singer. 2014. “Decoding Binary Node Labels from Censored Edge Measurements: Phase Transition and Efficient Recovery.” IEEE Trans. Network Sci. Eng. 1 (1):10–22. https://doi.org/10.1109/TNSE.2014.2368716.

Agarwal, A., and L. Bottou. 2015. “A Lower Bound for the Optimization of Finite Sums.” In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6-11 July 2015, 78–86. http://leon.bottou.org/papers/agarwal-bottou-2015.

Allen-Zhu, Z. 2016. “Katyusha: The First Direct Acceleration of Stochastic Gradient Methods.” Preprint arXiv:1603.05953 (Version 5).

Arjevani, Y. 2017. “Limitations on Variance-Reduction and Acceleration Schemes for Finite Sums Optimization.” In Advances in Neural Information Processing Systems 30, edited by I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, 3543–52. Curran Associates, Inc. http://papers.nips.cc/paper/6945-limitations-on-variance-reduction-and-acceleration-schemes-for-finite-sums-optimization.pdf.

Bandeira, A.S., N. Boumal, and V. Voroninski. 2016. “On the Low-Rank Approach for Semidefinite Programs Arising in Synchronization and Community Detection.” In Proceedings of the 29th Conference on Learning Theory, COLT 2016, New York, Usa, June 23-26, 2016, 361–82. http://jmlr.org/proceedings/papers/v49/bandeira16.html.

Bartlett, P.L., M.I. Jordan, and J.D. McAuliffe. 2006. “Convexity, Classification, and Risk Bounds.” J. Amer. Statist. Assoc. 101 (473):138–56. https://doi-org.offcampus.lib.washington.edu/10.1198/016214505000000907.

Beck, A., and M. Teboulle. 2012. “Smoothing and First Order Methods: A Unified Framework.” SIAM J. Optim. 22 (2):557–80. https://doi.org/10.1137/100818327.

Bottou, L., and O. Bousquet. 2008. “The Tradeoffs of Large Scale Learning.” In Advances in Neural Information Processing Systems, 161–68. http://leon.bottou.org/publications/pdf/nips-2007.pdf.

Burke, J.V., and M.C. Ferris. 1995. “A Gauss-Newton Method for Convex Composite Optimization.” Math. Programming 71 (2, Ser. A):179–94. https://doi.org/10.1007/BF01585997.

Candès, E.J., X. Li, Y. Ma, and J. Wright. 2011. “Robust Principal Component Analysis?” J. ACM 58 (3):Art. 11, 37. https://doi.org/10.1145/1970392.1970395.

Candès, E.J., X. Li, and M. Soltanolkotabi. 2015. “Phase Retrieval via Wirtinger Flow: Theory and Algorithms.” IEEE Trans. Inform. Theory 61 (4):1985–2007. https://doi.org/10.1109/TIT.2015.2399924.

Carmon, Y., J.C. Duchi, O. Hinder, and A. Sidford. 2017a. “‘Convex Until Proven Guilty’: Dimension-Free Acceleration of Gradient Descent on Non-Convex Functions.” In Proceedings of the 34th International Conference on Machine Learning, 70:654–63.

Y. Carmon, J.C. Duchi, O. Hinder, and A. Sidford. Lower bounds for finding stationary points I. Preprint arXiv:1710.11606.

Cartis, C., N.I.M. Gould, and P.L. Toint. 2011. “On the Evaluation Complexity of Composite Function Minimization with Applications to Nonconvex Nonlinear Programming.” SIAM J. Optim. 21 (4):1721–39. https://doi.org/10.1137/11082381X.

Chambolle, A., and T. Pock. 2011. “A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging.” J. Math. Imaging Vision 40 (1):120–45. https://doi.org/10.1007/s10851-010-0251-1.

Chandrasekaran, V., S. Sanghavi, P. A. Parrilo, and A.S. Willsky. 2011. “Rank-Sparsity Incoherence for Matrix Decomposition.” SIAM J. Optim. 21 (2):572–96. https://doi.org/10.1137/090761793.

Chen, Y., and E.J. Candès. 2017. “Solving Random Quadratic Systems of Equations Is Nearly as Easy as Solving Linear Systems.” Comm. Pure Appl. Math. 70 (5):822–83. https://doi-org.offcampus.lib.washington.edu/10.1002/cpa.21638.

Davis, D. 2016. “SMART: The Stochastic Monotone Aggregated Root-Finding Algorithm.” Preprint arXiv:1601.00698.

Davis, D., D. Drusvyatskiy, and C. Paquette. 2017. “The Nonsmooth Landscape of Phase Retrieval.” Preprint arXiv:1711.03247.

Davis, D., and B. Grimmer. 2017. “Proximally Guided Stochastic Sbgradient Method for Nonsmooth, Nonconvex Problems.” Preprint, arXiv:1707.03505.

Defazio, A. 2016. “A Simple Practical Accelerated Method for Finite Sums.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 676–84. Curran Associates, Inc. http://papers.nips.cc/paper/6154-a-simple-practical-accelerated-method-for-finite-sums.pdf.

Defazio, A., F. Bach, and S. Lacoste-Julien. 2014. “SAGA: A Fast Incremental Gradient Method with Support for Non-Strongly Convex Composite Objectives.” In Advances in Neural Information Processing Systems 27, edited by Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger, 1646–54. Curran Associates, Inc.

Defazio, A., J. Domke, and T.S. Caetano. 2014. “Finito: A Faster, Permutable Incremental Gradient Method for Big Data Problems.” In ICML, 1125–33.

Drusvyatskiy, D., and A.S. Lewis. 2013. “Tilt Stability, Uniform Quadratic Growth, and Strong Metric Regularity of the Subdifferential.” SIAM J. Optim. 23 (1):256–67. https://doi.org/10.1137/120876551.

D. Drusvyatskiy and A.S. Lewis. 2016. “Error Bounds, Quadratic Growth, and Linear Convergence of Proximal Methods.” To Appear in Math. Oper. Res., arXiv:1602.06661.

Drusvyatskiy, D., B.S. Mordukhovich, and T.T.A. Nghia. 2014. “Second-Order Growth, Tilt-Stability, and Metric Regularity of the Subdifferential.” J. Convex Anal. 21 (4):1165–92.

Drusvyatskiy, D., and C. Paquette. 2016. “Efficiency of Minimizing Compositions of Convex Functions and Smooth Maps.” Preprint, arXiv:1605.00125.

Duchi, J.C., and F. Ruan. 2017a. “Solving (Most) of a Set of Quadratic Equalities: Composite Optimization for Robust Phase Retrieval.” Preprint arXiv:1705.02356.

J.C. Duchi and F. Ruan. 2017b. “Stochastic Methods for Composite Optimization Problems.” Preprint arXiv:1703.08570.

Eldar, Y.C., and S. Mendelson. 2014. “Phase Retrieval: Stability and Recovery Guarantees.” Appl. Comput. Harmon. Anal. 36 (3):473–94. https://doi.org/10.1016/j.acha.2013.08.003.

Frostig, R., R. Ge, S.M. Kakade, and A. Sidford. 2015. “Un-Regularizing: Approximate Proximal Point and Faster Stochastic Algorithms for Empirical Risk Minimization.” In Proceedings of the 32nd International Conference on Machine Learning (ICML).

Ghadimi, S., and G. Lan. 2013. “Stochastic First- and Zeroth-Order Methods for Nonconvex Stochastic Programming.” SIAM J. Optim. 23 (4):2341–68. https://doi.org/10.1137/120880811.

Güler, O. 1992. “New Proximal Point Algorithms for Convex Minimization.” SIAM J. Optim. 2 (4):649–64. https://doi-org.offcampus.lib.washington.edu/10.1137/0802032.

Hazan, E., and S. Kale. 2011. “Beyond the Regret Minimization Barrier: An Optimal Algorithm for Stochastic Strongly-Convex Optimization.” In Proceedings of the 24th Annual Conference on Learning Theory, edited by Sham M. Kakade and Ulrike von Luxburg, 19:421–36. Proceedings of Machine Learning Research. Budapest, Hungary: PMLR.

Johnson, R., and T. Zhang. 2013. “Accelerating Stochastic Gradient Descent Using Predictive Variance Reduction.” In Proceedings of the 26th International Conference on Neural Information Processing Systems, 315–23. NIPS’13. USA: Curran Associates Inc. http://dl.acm.org/citation.cfm?id=2999611.2999647.

Juditsky, A., and Y. Nesterov. 2014. “Deterministic and Stochastic Primal-Dual Subgradient Algorithms for Uniformly Convex Minimization.” Stoch. Syst. 4 (1):44–80. https://doi-org.offcampus.lib.washington.edu/10.1214/10-SSY010.

Lacoste-Julien, S., M. Schmidt, and F. Bach. 2012. “A Simpler Approach to Obtaining an \({O}(1/t)\) Convergence Rate for the Projected Stochastic Subgradient Method.” Arxiv arXiv:1212.2002.

Lan, G. 2015. “An Optimal Randomized Incremental Gradient Method.” arXiv:1507.02000.

Lemarechal, C., J.-J. Strodiot, and A. Bihain. 1981. “On a Bundle Algorithm for Nonsmooth Optimization.” In Nonlinear Programming, 4 (Madison, Wis., 1980), 245–82. Academic Press, New York-London.

Lewis, A.S., and S.J. Wright. 2015. “A Proximal Method for Composite Minimization.” Math. Program. Springer Berlin Heidelberg, 1–46. https://doi.org/10.1007/s10107-015-0943-9.

Lin, H., J. Mairal, and Z. Harchaoui. 2015. “A Universal Catalyst for First-Order Optimization.” In Advances in Neural Information Processing Systems, 3366–74.

Lin, H., J. Mairal, and Z. Harchaoui. “Catalyst Acceleration for First-order Convex Optimization: from Theory to Practice.” arXiv preprint arXiv:1712.05654 (2017).

Luke, R. 2017. “Phase Retrieval, What’s New?” SIAG/OPT Views and News 25 (1).

Mairal, J. 2015. “Incremental Majorization-Minimization Optimization with Application to Large-Scale Machine Learning.” SIAM Journal on Optimization 25 (2):829–55.

Nemirovski, A. 2004. “Prox-Method with Rate of Convergence \(O(1/t)\) for Variational Inequalities with Lipschitz Continuous Monotone Operators and Smooth Convex-Concave Saddle Point Problems.” SIAM J. Optim. 15 (1):229–51. https://doi.org/10.1137/S1052623403425629.

Nemirovski, A., A. Juditsky, G. Lan, and A. Shapiro. 2008. “Robust Stochastic Approximation Approach to Stochastic Programming.” SIAM J. Optim. 19 (4):1574–1609. https://doi-org.offcampus.lib.washington.edu/10.1137/070704277.

Nemirovsky, A.S., and D.B. Yudin. 1983. Problem Complexity and Method Efficiency in Optimization. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York.

Nesterov, Y., and A. Nemirovskii. 1994. Interior-Point Polynomial Algorithms in Convex Programming. Vol. 13. SIAM Studies in Applied Mathematics. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611970791.

Nesterov, Yu. 1983. “A Method for Solving the Convex Programming Problem with Convergence Rate \(O(1/k^{2})\).” Dokl. Akad. Nauk SSSR 269 (3):543–47.

Nesterov, Yu. 2005. “Smooth Minimization of Non-Smooth Functions.” Math. Program. 103 (1, Ser. A):127–52. https://doi.org/10.1007/s10107-004-0552-5.

Nesterov, Yu. 2007. “Modified Gauss-Newton Scheme with Worst Case Guarantees for Global Performance.” Optim. Methods Softw. 22 (3):469–83. https://doi.org/10.1080/08927020600643812.

Nesterov, Yu. 2013. “Gradient Methods for Minimizing Composite Functions.” Math. Program. 140 (1, Ser. B):125–61. https://doi.org/10.1007/s10107-012-0629-5.

Paquette, C., H. Lin, D. Drusvyatskiy, J. Mairal, and Z. Harchaoui. 2017. “Catalyst Acceleration for Gradient-Based Non-Convex Optimization.” Preprint arXiv:1703.10993.

Polyak, B.T., and A.B. Juditsky. 1992. “Acceleration of Stochastic Approximation by Averaging.” SIAM J. Control Optim. 30 (4):838–55. https://doi.org/10.1137/0330046.

Rakhlin, A., O. Shamir, and K. Sridharan. 2012. “Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization.” In Proceedings of the 29th International Coference on International Conference on Machine Learning, 1571–8. ICML’12. USA: Omnipress. http://dl.acm.org/citation.cfm?id=3042573.3042774.

Robbins, H., and S. Monro. 1951. “A Stochastic Approximation Method.” Ann. Math. Statistics 22:400–407.

Schmidt, M., N. Le Roux, and F. Bach. 2013. “Minimizing Finite Sums with the Stochastic Average Gradient.” arXiv:1309.2388.

Shalev-Shwartz, S., and T. Zhang. 2012. “Proximal Stochastic Dual Coordinate Ascent.” arXiv:1211.2717.

S. Shalev-Shwartz and T. Zhang. 2015. “Accelerated Proximal Stochastic Dual Coordinate Ascent for Regularized Loss Minimization.” Mathematical Programming.

Singer, A. 2011. “Angular Synchronization by Eigenvectors and Semidefinite Programming.” Appl. Comput. Harmon. Anal. 30 (1):20–36. https://doi.org/10.1016/j.acha.2010.02.001.

Sun, J., Q. Qu, and J. Wright. 2017. “A Geometric Analysis of Phase Retrieval.” To Appear in Found. Comp. Math., arXiv:1602.06664.

Woodworth, B.E., and N. Srebro. 2016. “Tight Complexity Bounds for Optimizing Composite Objectives.” In Advances in Neural Information Processing Systems 29, edited by D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon, and R. Garnett, 3639–47. Curran Associates, Inc. http://papers.nips.cc/paper/6058-tight-complexity-bounds-for-optimizing-composite-objectives.pdf.

Wright, S.J. 1997. Primal-Dual Interior-Point Methods. Society for Industrial; Applied Mathematics (SIAM), Philadelphia, PA. https://doi.org/10.1137/1.9781611971453.

Xiao, L., and T. Zhang. 2014. “A Proximal Stochastic Gradient Method with Progressive Variance Reduction.” SIAM J. Optim. 24 (4):2057–75. https://doi.org/10.1137/140961791.