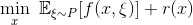In this blog, we discuss our recent paper, (Davis and Drusyatskiy, 2018). This work proves that the proximal stochastic subgradient method converges at a rate \(O(k^{-1/4})\) on weakly convex problems. In particular, it resolves the long-standing open question on the rate of convergence of the proximal stochastic gradient method (without batching) for minimizing a sum of a smooth function and a proximable convex function.
Introduction
Stochastic optimization is a fundamental task in the statistical sciences, underlying all aspects of learning from data. The goal of stochastic optimization in data science is to learn a decision rule from a limited data sample, which generalizes well to the entire population. Learning such a decision rule amounts to minimizing the population risk:
\[\begin{align}\label{eqn:SO} \min_{x \in \mathbb{R}^d}~ \mathbb{E}_{\xi\sim P}[f(x,\xi)].\tag{$\mathcal{SO}$} \end{align}\]Here, \(\xi\) encodes the population data, which is assumed to follow some fixed but unknown probability distribution \(P\), and the function \(f(x,\xi)\) evaluates the loss of the decision rule parametrized by \(x\) on a data point \(\xi\).
Robbins-Monro’s pioneering 1951 work gave the first procedure for solving (\ref{eqn:SO}) when \(f(\cdot, \xi)\) are smooth and strongly convex, inspiring decades of further research. Among such algorithms, the stochastic (sub)gradient method is the most successful and widely used in practice. This method constructs a sequence of approximations \(x_t\) of the minimizer of (\ref{eqn:SO}) by traveling in the direction negative to a sample gradient:
\[\begin{equation*}\label{eqn:SG} \textrm{Sample } \xi_t \sim P \\ \textrm{Set } x_{t+1}= x_t - \alpha_t \nabla_x f(x_t, \xi_t),\tag{$\mathcal{SG}$} \end{equation*}\]where \(\alpha_t>0\) is an appropriately chosen control sequence. Nonsmooth convex problems may be similarly optimized by replacing sample gradients by sample subgradients \(v_t\in \partial_x f(x_t,\xi_t)\), where \(\partial_x f(x_t, \xi_t)\) is the subdifferential in the sense of convex analysis; see for example, Part V in (Rockafellar, 1970).
Performance of stochastic optimization methods is best judged by their sample complexity – the number of i.i.d. realizations \(\xi_1, \ldots, \xi_N \sim P\) needed to reach a desired accuracy of the decision rule. Classical results such as by (Nemirovsky and Yudin, 1983) stipulate that for convex problems, it suffices to generate \(O(\varepsilon^{-2})\) samples to reach functional accuracy \(\varepsilon\) in expectation, and this complexity is unimprovable without making stronger assumptions.
While the sample complexity of the stochastic subgradient method is well-understood for convex problems, much less is known for nonconvex problems. In particular, the sample complexity of the method is not yet known for any reasonably wide class of problems beyond those that are smooth or convex. This is somewhat concerning as the stochastic subgradient method is the simplest and most widely used stochastic optimization algorithm for large-scale problems arising in machine learning and is the core optimization subroutine in industry backed software libraries, such as Google’s TensorFlow.
In the recent paper (Davis and Drusvyatskiy, 2018), we aim to close the gap between theory and practice and provide the first sample complexity bounds for the stochastic subgradient method applied to a large class of nonsmooth and nonconvex optimization problems. The problem class we consider captures a variety of important computational tasks in data science, as described below.
Our guarantees apply to an even broader setting than population risk minimization (\ref{eqn:SO}). Indeed, numerous tasks in machine learning and high dimensional statistics yield problems of the form
\[\begin{equation}\label{eqn:gen_err} \min_{x\in\mathbb{R}^d}~ \varphi(x)=g(x)+r(x),\tag{$\mathcal{P}$} \end{equation}\]where the functional components \(g\) and \(r\) play qualitatively different roles. The function \(g\colon\mathbb{R}^d\to\mathbb{R}\) plays a similar role to the population risk in (\ref{eqn:SO}). We will assume that the only access to \(g\) is through stochastic estimates of its (generalized) gradients. That is, given a point \(x\), one can generate a random vector \(v\in\mathbb{R}^d\) satisfying \(\mathbb{E}[v]\in \partial g(x)\). A formal definition of the nonconvex subdifferential \(\partial g(x)\) is standard in the optimization literature; see Definition 8.3 in (Rockafellar and Wets, 1998). The exact details will not be important for the blog. We note however that when \(g\) is differentiable at \(x\), the subdifferential \(\partial g(x)\) consists only of the gradient \(\nabla g(x)\), while for convex functions, it reduces to the subdifferential in the sense of convex analysis.
In contrast, we assume the function \(r\colon\mathbb{R}^d\to\mathbb{R}\cup\{+\infty\}\) to be explicitly known and simple. It is often used to model constraints on the parameters \(x\) or to encourage \(x\) to have some low dimensional structure, such as sparsity or low rank. Within a Bayesian framework, the regularizer \(r\) can model prior distributional information on \(x\). One common assumption, which we also make here, is that \(r\) is closed and convex and admits a computable proximal map
\[\begin{equation*} {\rm prox}_{\alpha r}(x):= \underset{y}{\operatorname{argmin}}\, \left\{r(y)+\tfrac{1}{2\alpha}\|y-x\|^2\right\}. \end{equation*}\]In particular, when \(r\) is an indicator function of a closed convex set – meaning it equals zero on it and is \(+\infty\) off it – the proximal map \({\rm prox}_{\alpha r}(\cdot)\) reduces to the nearest-point projection.
The most widely used algorithm for (\ref{eqn:gen_err}) is a direct generalization of (\ref{eqn:SG}), called the proximal stochastic subgradient method. Given a current iterate \(x_t\), the method performs the update
\[\begin{equation*}\left\{ \begin{aligned} &\textrm{Generate a stochastic subgradient } v_t\in\mathbb{R}^d \textrm{ of } g \textrm{ at } x_t\\ & \textrm{Set } x_{t+1}={\rm prox}_{\alpha_t r}\left(x_{t} - \alpha_t v_t\right) \end{aligned}\right\}, \end{equation*}\]where \(\alpha_t>0\) is an appropriately chosen control sequence.
The search for stationary points
Convex optimization algorithms are judged by the rate at which they decrease the function value along the iterate sequence. Analysis of smooth optimization algorithms focuses instead on the magnitude of the gradients along the iterates. The situation becomes quite different for problems that are neither smooth nor convex.
The primary goal, akin to smooth minimization, is the search for stationary points. A point \(x\in\mathbb{R}^d\) is called stationary for the problem (\ref{eqn:gen_err}) if the inclusion \(0\in \partial \varphi(x)\) holds. In “primal terms”, these are precisely the points where the directional derivative of \(\varphi\) is nonnegative in every direction. Indeed, under mild conditions on \(\varphi\), equality holds; see Proposition 8.32 in (Rockafellar and Wets, 1998):
\[\begin{equation*} %\label{eqn:subdif_direc_der} {\rm dist}(0;\partial \varphi(x))=-\inf_{v:\, \|v\|\leq 1} \varphi'(x;v). \end{equation*}\]Thus a point \(x\), satisfying \({\rm dist}(0;\partial \varphi(x))\leq \varepsilon\), approximately satisfies first-order necessary conditions for optimality.
An immediate difficulty in analyzing stochastic subgradient methods for nonsmooth and nonconvex problems is that it is not a priori clear how to measure the progress of the algorithm. Neither the functional suboptimality gap, \(\varphi(x_t)-\min \varphi\), nor the stationarity measure, \({\rm dist}(0;\partial \varphi(x_t))\), necessarily tend to zero along the iterate sequence. Indeed, what is missing is a continuous measure of stationarity to monitor, instead of the highly discontinuous function \(x\mapsto{\rm dist}(0;\partial \varphi(x))\).
Weak convexity and the Moreau envelope
In the work (Davis and Drusvyatskiy, 2018), we focus on a class of problems that naturally admit a continuous measure of stationarity. We assume that \(g\colon\mathbb{R}^d\to\mathbb{R}\) is a \(\rho\)-weakly convex function, meaning that the assignment \(x\mapsto g(x)+\frac{\rho}{2}\|x\|^2\) is convex. The class of weakly convex functions is broad. It includes all convex functions and smooth functions with Lipschitz continuous gradient. More generally, any function of the form \(g = h\circ c,\) with \(h\) convex and \(L\)-Lipschitz and \(c\) a smooth map with \(\beta\)-Lipschitz Jacobian, is weakly convex with constant \(\rho\leq L\beta\) ; see Lemma 4.2 in (Drusvyatskiy and Paquette, 2016). Notice that such composite functions need not be smooth nor convex. Classical literature highlights the importance of weak convexity in optimization (Rockafellar, 1982; Poliquin and Rockafellar, 1992; Poliquin and Rockafellar, 1996), while recent advances in statistical learning and signal processing have further reinvigorated the problem class. Nonlinear least squares, phase retrieval (Eldar and Mendelson, 2014; Duchi and Ruan, 2017; Davis, Drusvyatskiy, and Paquette, 2017), graph synchronization (Bandeira, Boumal, and Voroninski, 2016; Singer, 2011; Abbe, Bandeira, Bracher, and Singer, 2014), and robust principal component analysis (Candès, Li, Ma, and Wright, 2011; Chandrasekaran, Sanghavi, Parrilo, and Willsky, 2011) naturally lead to weakly convex formulations. For a recent discussion on the role of weak convexity in large-scale optimization, see e.g., (Drusvyatskiy, 2018) or the previous blog post.
It has been known since Nurminskii’s work (Nurminskii, 1974; Nurminskii 1973) that when \(g\) is \(\rho\)-weakly convex and \(r=0\), the stochastic subgradient method generates an iterate sequence that subsequentially converges to a stationary point of the problem, almost surely. Nonetheless, the sample complexity of the basic method and of its proximal extension, has remained elusive. Our approach to resolving this open problem relies on the elementary observation: weakly convex problems naturally admit a continuous measure of stationarity through implicit smoothing. The key construction we use is the Moreau envelope:
\[\varphi_{\lambda}(x):=\min_{y}~ \left\{\varphi(y)+\tfrac{1}{2\lambda}\|y-x\|^2\right\},\]where \(\lambda > 0\). Standard results such as Theorem 31.5 in (Rockafellar, 1970) show that as long as \(\lambda<\rho^{-1}\), the envelope \(\varphi_{\lambda}\) is \(C^1\)-smooth with the gradient given by
\[\begin{equation}\label{eqn:grad_form} \nabla \varphi_{\lambda}(x)=\lambda^{-1}(x-{\rm prox}_{\lambda \varphi}(x)). \end{equation}\]When \(r=0\) and \(g\) is smooth, the norm \(\|\nabla \varphi_{\lambda}(x)\|\) is proportional to the magnitude of the true gradient \(\|\nabla g(x)\|\). In the broader nonsmooth setting, the norm of the gradient \(\|\nabla \varphi_{\lambda}(x)\|\) has an intuitive interpretation in terms of near-stationarity for the target problem (\ref{eqn:gen_err}). Namely, the definition of the Moreau envelope directly implies that for any point \(x\in\mathbb{R}^d\), the proximal point \(\hat x:={\rm prox}_{\lambda \varphi}(x)\) satisfies
\[\begin{equation*} \left\{\begin{array}{cl} \|\hat{x}-x\|&= \lambda\|\nabla \varphi_{\lambda}(x)\|,\\ %F(\hat x)-F(S_t(x))&\leq \frac{t}{2}(L\beta t+1)\|\mathcal{G}_t(x)\|^2,\\ \varphi(\hat x) &\leq \varphi(x),\\ {\rm dist}(0;\partial \varphi(\hat{x}))&\leq \|\nabla \varphi_{\lambda}(x)\|. \end{array}\right. \end{equation*}\]Thus a small gradient \(\|\nabla \varphi_{\lambda}(x)\|\) implies that \(x\) is near some point \(\hat x\) that is nearly stationary for (\ref{eqn:gen_err}). For a longer discussion of the near-stationarity concept, see (Drusvyatskiy, 2018; Section 4.1 in Drusvyatskiy and Paquette, 2016), or the previous blog post.
Contributions
In the paper (Davis and Drusvyatskiy, 2018), we show that under an appropriate choice of the sequence \(\alpha_t\), the proximal stochastic subgradient method will generate a point \(x\) satisfying \(\mathbb{E}\|\nabla \varphi_{1/(2\rho)}(x)\|\leq \varepsilon\) after at most \(O(\varepsilon^{-4})\) iterations.1This is perhaps surprising, since neither the Moreau envelope \(\varphi_{\lambda}(\cdot)\) nor the proximal map \({\rm prox}_{\lambda \varphi}(\cdot)\) explicitly appear in the definition of the stochastic subgradient method. Our work appears to be the first to recognize the Moreau envelope as a useful potential function for analyzing subgradient methods.
The convergence guarantees we develop are new even in simplified cases. Two such settings are (a) when \(g\) is smooth and \(r\) is the indicator function of a closed convex set, and (b) when \(g\) is nonsmooth, \(r = 0\), and we have explicit access to the exact subgradients of \(g\).
Related Literature and Context
Analogous convergence guarantees when \(r\) is an indicator function of a closed convex set were recently established for a different algorithm in (Davis and Grimmer, 2017), called the proximally guided projected subgradient method. This scheme proceeds by directly applying the gradient descent method to the Moreau envelope \(\varphi_{\lambda}\), with each proximal point \({\rm prox}_{\lambda \varphi}(x)\) approximately evaluated by a convex subgradient method. In contrast, we showed that the basic stochastic subgradient method in the fully proximal setting, and without any modification or parameter tuning, already satisfies the desired convergence guarantees.
Our work also improves in two fundamental ways on the results in the seminal papers on the stochastic proximal gradient method for smooth functions (Ghadimi and Lan, 2013; Ghadimi, Lan, and Zhang, 2016; Xu and Yin, 2015): first, we allow \(g\) to be nonsmooth and second, even when \(g\) is smooth we do not require the variance of our stochastic estimator for \(\nabla g(x_t)\) to decrease as a function of \(t\). The second contribution removes the well-known “mini-batching” requirements common to (Ghadimi, Lan, and Zhang, 2016; Xu and Yin, 2015), while the first significantly expands the class of functions for which the rate of convergence of the stochastic proximal subgradient method is known.
The results in this paper are orthogonal to the recent line of work on accelerated rates of convergence for smooth nonconvex finite sum minimization problems, e.g.,(Lei, Ju, Chen, and Jordan, 2017; Katyusha, Allen-Zhu, 2017; Reddi, Sra, Poczos, Smola, 2016; Natasha 2, Allen-Zhu, 2017). These works crucially exploit the finite sum structure and/or (higher order) smoothness of the objective functions to push beyond the \(O(\varepsilon^{-4})\) complexity. We leave it as an intriguing open question whether such improvement is possible for the nonsmooth weakly convex setting we consider here.
References
E. Abbe, A.S. Bandeira, A. Bracher, and A. Singer. Decoding binary node labels from censored edge measurements: phase transition and efficient recovery. IEEE Trans. Network Sci. Eng., 1(1):10-22, 2014.
Z. Allen-Zhu. Katyusha: The First Direct Acceleration of Stochastic Gradient Methods. In STOC, 2017.
Z. Allen-Zhu. Natasha 2: Faster non-convex optimization than sgd. arXiv preprint arXiv:1708.08694, 2017.
Z. Allen-Zhu. How to make gradients small stochastically. Preprint arXiv:1801.02982 (version 1), 2018.
A.S. Bandeira, N. Boumal, and V. Voroninski. On the low-rank approach for semidefinite programs arising in synchronization and community detection. In Proceedings of the 29th Conference on Learning Theory, COLT 2016, New York, June 23-26, 2016, pages 361-382, 2016.
E.J. Candès, X. Li, Y. Ma, and J. Wright. Robust principal component analysis? J. ACM, 58(3):Art. 11, 37, 2011.
V. Chandrasekaran, S. Sanghavi, P. A. Parrilo, and A.S. Willsky. Rank-sparsity incoherence for matrix decomposition. SIAM J Optim., 21(2):572-596, 2011.
D. Davis and D. Drusvyatskiy. Complexity of finding near-stationary points of convex functions stochastically. arXiv:1802.08556, 2018.
D. Davis and D. Drusvyatskiy. Stochastic subgradient method converges at the rate $(O(k^{-1/4})$ on weakly convex functions. arXiv: 1802.02988, 2018.
D. Davis, D. Drusvyatskiy, and C. Paquette. The nonsmooth landscape of phase retrieval. Preprint arXiv:1711.03247, 2017.
D. Davis and B. Grimmer. Proximally guided stochastic method for nonsmooth, non-convex problems. Preprint arXiv:1707.03505, 2017.
D. Drusvyatskiy. The proximal point method revisited. To appear in the SIAG/OPT Views and News, arXiv:1712.06038, 2018.
D. Drusvyatskiy and C. Paquette. Efficiency of minimizing compositions of convex functions and smooth maps. Preprint arXiv:1605.00125, 2016.
J.C. Duchi and F. Ruan. Solving (most) of a set of quadratic equalities: Composite optimization for robust phase retrieval. Preprint arXiv:1705.02356, 2017.
Y.C. Eldar and S. Mendelson. Phase retrieval: stability and recovery guarantees. Appl. Comput. Harmon. Anal., 36(3):473-494, 2014.
S. Ghadimi and G. Lan. Stochastic first- and zeroth-order methods for nonconvex stochastic programming. SIAM J. Optim., 23(4):2341-2368, 2013.
S. Ghadimi, G. Lan, and H. Zhang. Mini-batch stochastic approximation methods for nonconvex stochastic composite optimization, Math. Program., 155(1):267-305, 2016.
L. Lei, C. Ju, J. Chen, and M.I Jordan. Non-convex finite-sum optimization via scsg methods. In Advances in Neural Information Processing Systems, pages 2345-2355, 2017.
A.S. Nemirovsky and D.B. Yudin. Problem complexity and method efficiency in optimization. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York, 1983.
E. A. Nurminskii. The quasigradient method for the solving of the nonlinear programming problems. Cybernetics, 9(1):145-150, Jan 1973.
E. A. Nurminskii. Minimization of nondifferentiable functions in the presence of noise. Cybernetics, 10(4):619-621, Jul 1974.
R.A. Poliquin and R.T. Rockafellar. Amenable functions in optimization. In Nonsmooth optimization: methods and applications (Erice, 1991), pages 338-353. Gordon and Breach, Montreaux, 1992.
R.A. Poliquin and R.T. Rockafellar. Prox-regular functions in variational analysis. Trans. Amer. Math. Soc., 348:1805-1838, 1996.
Sashank J Reddi, Suvrit Sra, Barnabas Poczos, and Alexander J Smola. Proximal stochastic methods for nonsmooth nonconvex finite-sum optimization. In Advances in Neural Information Processing Systems, pages 1145-1153, 2016.
R.T. Rockafellar. Convex Analysis. Princeton University Press, 1970.
R.T. Rockafellar. Favorable classes of Lipschitz-continuous functions in subgradient optimization. In Progress in nondifferentiable optimization, volume 8 of IIASA Collaborative Proc. Ser. CP-82, pages 125-143. Int. Inst. Appl. Sys. Anal., Laxenburg, 1982.
R.T. Rockafellar and R.J-B. Wets. Variational Analysis. Grundlehren der mathemtischen Wissenschaften, Vol 317, Springer, Berlin, 1998.
A. Singer. Angular synchronization by eigenvectors and semidefinite programming. Appl. Comput. Harmon. Anal., 30(1):20-36, 2011.
Y. Xu and W. Yin. Block stochastic gradient iteation for convex and nonconvex optimization. SIAM J. Optim., 25(3):1686-1716, 2015.
-
In the supplementary text (Davis and Drusvyatskiy, 2018), we also showed that when \(g\) happens to be convex, this complexity can be improved to \(\widetilde{O}(\varepsilon^{-2})\) by adapting a gradual regularization technique of (Allen-Zhu, 2018). ↩